حقوق الطبع لهذا البحث محفوظة للمشروع الإسلامي لرصد الأهلة © 2007

المواد غير قابلة لإعادة النشر دون إذن مسبق

---

تحديد اتجاه القبلة

بواسطة الإسطرلاب

تحديد اتجاه القبلة

بواسطة الإسطرلاب

 

أ. د. حسن بيلاني

أستاذ الجيوديزيا في كلية الهندسة - جامعة الملك سعود بالرياض

الملخص

إن الاتجاه نحو الكعبة المشرفة، يعتبر شرط أساسي لصحة عبادة الصلاة. وهذا الشرط يتحقق بتطبيق القوانين الرياضية في المثلثات الكروية.

وحتى ظهور الحاسبات الإلكترونية، اعتبرت مسألة حل المثلث الكروي مسألة معقدة. إلا أن الإسطرلاب كان بالفعل حاسوب عصره، حيث أمكن بواسطته حل العديد من المسائل الفلكية المعقدة، مثل قياس الارتفاعات والأعماق وزوايا الارتفاع وأوقات الصلاة واتجاه القبلة وغيرها.

ويعتمد مبدأ حل المثلث الكروي بالإسطرلاب على محاكاة الفراغ الثلاثي البعد (قبة السماء) في مستوي ثنائي البعد. وتعتبر المحاكاة حالياً من الأساليب الحديثة في استخدام الحاسوب الإلكتروني لحل المسائل العلمية المختلفة.

وبغية إظهار إبداع الحضارة الإسلامية في هذا المجال، تم في هذه الورقة دراسة مسألة تحديد اتجاه القبلة باستخدام الإسطرلاب، وذلك من خلال تحليل هندسي للمنحنيات المرسومة على وجه الإسطرلاب وظهره.

 

 

كلمات مفتاحية:

 إسطرلاب، اتجاه القبلة

تمهيد

تعتبر مسائل دراسة حركة الشمس الظاهرية وتحديد الاتجاهات على سطح الكرة من أهم مسائل علم المثلثات الكروية. واتخذت هذه المسائل أهمية خاصة في الشريعة الإسلامية، من خلال ارتباط عبادة الصلاة، بتحديد اتجاه أساسي على سطح الأرض، هو اتجاه مدينة مكة المكرّمة (اتجاه القبلة)، وبتحديد زمن عبور الشمس لنقاط محددة في القبة السماوية.

وتقسم هذه المسائل إلى مرحلتين: الأولى تتمثل بالحساب، والثانية تتمثل بتجسيد نتائج الحساب على الواقع. وقد كان الإسطرلاب يقوم بهاتين المرحلتين.

 

الإسطرلاب المسطحّ

آلة فلكية معظم نماذجها صغيرة الحجم وسهلة الحمل، استخدمت كآلة رصد يمكن بواسطتها تحديد الانحرافات الشاقولية والأفقي، و كآلة حساب يمكنها حل المئات من المسائل الفلكية والحسابية المرتبطة بالرصد. حيث يقوم بدور آلة رصد (تيودولايت)، وآلة حساب، وحتى يمكن القول بأنه يقوم بحل بعض المسائل كما تقوم به الآلات الحاسبة المبرمجة. وهناك ناحية أخرى هي إمكانية حل المسائل مباشرة، والحصول على النتيجة من الإسطرلاب نفسه، دون الحاجة لتدوين أي شيء على الورق.

 استخدم الإسطرلاب المسطّح في الملاحة إبّان الحضارة الإسلامية، ثم استخدم فيما بعد في رحلات المستكشفين، بعد أن تسرب علم الإسطرلاب وكيفية صناعته من الأندلس إلى أوربا. 

إنّ مبدأ تصميم الإسطرلاب يعتمد على نظام الإسقاط الستيريوغرافي الذي يحول الفلك الكروي (الثلاثي البعد) إلى فلك مستوي (الثنائي البعد) كما يلي:

1- إسقاط نظام الإحداثيات الاستوائي على مستو بطريقة الإسقاط الستيريوغرافي.

2- إسقاط النقاط التي تمثل النجوم والكواكب المعروفة على نفس المستوي.

3- يصنع من هذا المستوي صفيحة دائرية معدنية مفرغة تسمى الشبكة أو العنكبوت، بحيث تحوي نهايات مدببة (مري نجوم) تمثل تلك النجوم وموقعها. بذلك أصبحت هذه الصفيحة تمثل مسقط كرة الفلك على سطح مستو (الشكل 1). بإعطاء حرية الدوران لهذه الصفيحة حول محورها، يكون قد تحقق مسقط الدوران الظاهري لكرة الفلك، الناجم عن دوران الأرض.

4- يتم إسقاط دائرة الأفق والدوائر الموازية لها ودوائر الارتفاع، ولكن على مستو آخر، وهي صفيحة معدنية دائرية، ينطبق محورها مع محور الشبكة، إلا أنها ثابتة لا تدور معها. توضع هذه الصفيحة تحت الشبكة بحيث تظهر منحنياتها من خلال الفراغات في الشبكة. الآن بدوران الشبكة (العنكبوت)، تتحرك النهايات المدببة التي تمثل نجوماً معروفة، بالنسبة لمسقط منظومة الإحداثيات الكروية (القسم الغير مظلل في الشكل 1)، فيتمثل لدينا وضع محاكي لقبة السماء، حيث تشرق نجوم وكواكب وتغيب أخرى، وشكل هذه اللوحة المتحركة في قبة السماء يختلف تبعاً لنقطة الرصد، وبالتحديد تبعاً للعرض الجغرافي. وطبعاً هناك نجوم لا تغيب أبداً، وهذا يتوقف على موقع الراصد. هذه النجوم تتحدد فلكياً بأنها ذات زاوية الانحراف d التي تحقق الشرط:  (j-90) ³ d، حيثj  عرض موقع الرصد.

إذاً بأي وضعية كانت الصفيحة العلوية (العنكبوت)، فكل نجم يعرف بمجموعتي إحداثيات: الأولى منسوبة للنظام الاستوائي الذي تمثله مواقع النهايات المدببة في العنكبوت. والثانية منسوبة للنظام الأفقي (Topocentric)، وتسمى جملة الإحداثيات المائلة لأنها ترتبط بموقع الراصد.

 

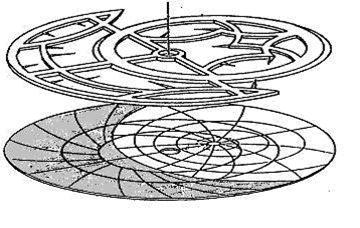
الشكل 1

وهناك منحنيات أخرى في الصفيحة تمثل الساعات، وترسم هذه المنحنيات بتقسيم أقواس دوائر السرطان والاستواء والجدي الواقعة تحت خط الأفق (الشكل 2) إلى اثني عشر قسماً متساوياً، ومن ثم وصل هذه الأقسام بمنحني دائري.

 

 

 

 

 

 

 

 

 

 

 

 

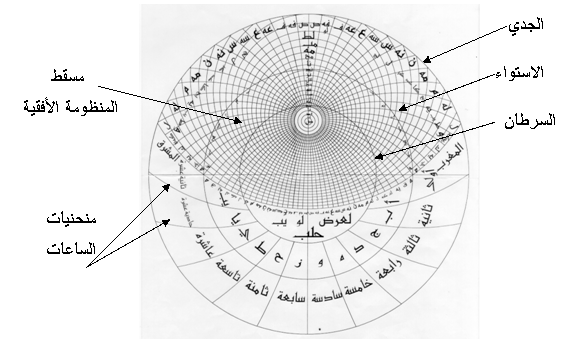
الشكل 2

 

إن الصفيحة السفلية تمثل النظام الإحداثي الأفقي الخاص بعرض جغرافي معين. ويمكن صنع العديد من هذه الصفائح لعروض أخرى ووضعها ضمن الحجرة بحيث تكون الصفيحة العلوية منها هي التي سيتم القياس فيها (الشكل 3).

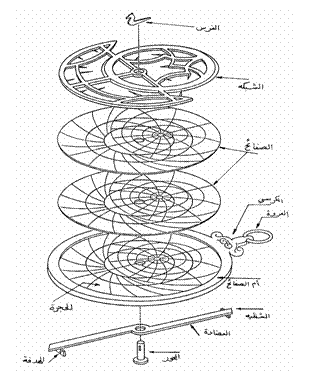
الشكل 3

أهمية البحث

على مدى قرون، استخدم الإسطرلاب كأداة لحساب وتحديد أوقات الصلاة واتجاه القبلة. و يعتمد حل تلك المسائل، كما هو معلوم، على قوانين المثلث الكروي. وكان الإسطرلاب يقوم بحل تلك القوانين بسرعة وسهولة باعتماد أسلوب المحاكاة. وتتجلّى أهمية هذا البحث في إجراء تحليل هندسي لحل تلك المسائل بواسطة أهم آلة فلكية تراثية، خاصة وأن معظم الدراسات السابقة تناولت الإسطرلاب بشكل وصفي دون تحليل هندسي.

 

تحديد اتجاه القبلة بواسطة الإسطرلاب ليلاً

من المعلوم أنه في أي مثلث كروي يربط بين القطب ونقطتين /1/ و /2/ تتحقق العلاقتان الآتيتان (الشكل 4):

فإذا نسبنا هاتين المعادلتين إلى بعضيهما مع اعتبار أن النقطة /1/ تمثل مكان تحديد القبلة ذو الإحداثيات ، والنقطة /2/ تمثل مكة المكرمة ذات الإحداثيات  نحصل على العلاقة الآتية:

 

 

 

 

 

 

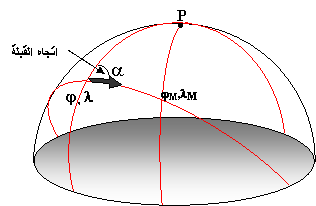
)الشكل 4)

إن هذه العلاقة تحل مرة واحدة بالنسبة للمدينة الواحدة، ثم تأتي مهمة تجسيد اتجاه القبلة، اعتماداً على قيمة a، وهذا يعني الاعتماد على القطب الشمالي، مع توفر جهاز قادر على قياس زاوية أفقية وهذا يتم بواسطة الإسطرلاب كالآتي:

·   إسقاط اتجاه نجم القطب على الأفق بواسطة العضادة، حيث بعد التسديد باتجاه نجم القطب تدار العضادة مع المحافظة على اتجاه الإسطرلاب حتى تصبح أفقية تقريباً بحيث نضع إشارة مضيئة على الأرض، بذلك يمثل المستقيم الواصل بين نقطة الوقوف والإشارة اتجاه الشمال مجسداً على الأرض.

·   يوضع الإسطرلاب أفقياً، وتسدد العضادة على اتجاه الإشارة وتقرأ الزاوية عند رأس العضادة (مري العضادة).

·   تدار العضادة حتى التدريجة التي تزيد عن السابقة بالزاوية a. الآن أصبح اتجاه العضادة باتجاه القبلة فتوضع إشارة على ذلك الاتجاه (الشكل 5).

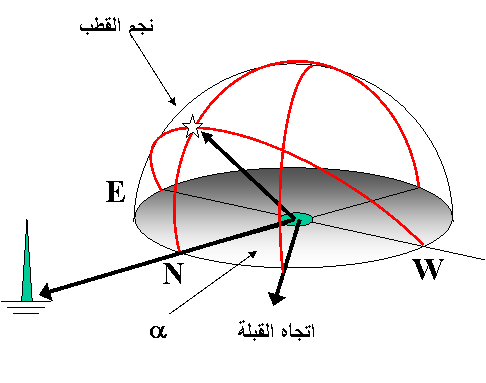
الشكل 5

 

هذا يعني أن هناك مرحلتان من القياس: الأولى باستخدام الإسطرلاب بوضع رأسي لإسقاط نجم القطب، والثانية باستخدام الإسطرلاب بوضع أفقي لتجسيد a، وهذا يؤدي إلى تراكم أخطاء القياس التي تنعكس على الدقة، بالإضافة إلى الخطأ الناجم من عدم تطابق نجم القطب مع القطب الشمالي. ولكن إجمالاً يمكن القول أن المسألة تحل اعتماداً على النجوم باستخدام الإسطرلاب كجهاز تيودولايت.

 

تحديد اتجاه القبلة بواسطة الإسطرلاب نهاراً

لندرس تحديد اتجاه القبلة بالنسبة لراصد موجود في المنطقة الشمالية للكرة الأرضية. في هذه الحالة، وفي كل يوم، في لحظة ما، سينطبق اتجاه الشمس مع اتجاه القبلة، بالنسبة لراصد ينظر باتجاه الجنوب (الشكل 6). فهناك إذاً علاقة بين اتجاه القبلة وارتفاع الشمس عن الأفق والزمن.

 

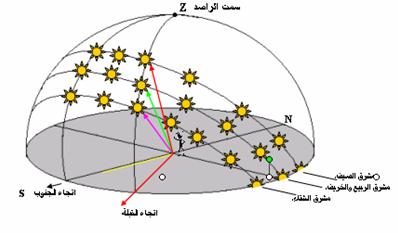
(الشكل 6)

 

ومن الشكل (7) نلاحظ تشكل هذه العلاقة من المثلث الكروي ZPS حيث يمثل انحراف الشمس d وسيطاً دالاً على الزمن. وتعطى العلاقة الموصوفة أعلاه بالشكل الآتي:

حيث h ارتفاع الشمس.

وباعتبار أن اتجاه القبلة والعرض الجغرافي ثوابت في هذه المعادلة، تبقى العلاقة بين الزمن (بالأيام) وارتفاع الشمس الدال على القبلة

 

 

 

 

 

 

 

 

 

 

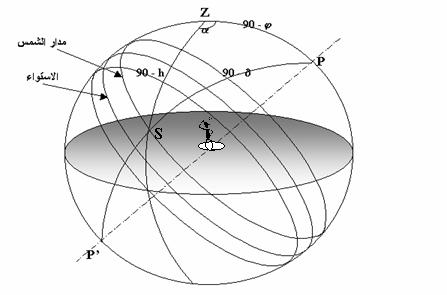
الشكل (7)

 

إن حل المعادلة السابقة يعتمد على فرض عدة قيم للانحراف d، الذي يعني الزمن من أجل الحصول على القيم الموافقة من الارتفاع h. ورياضياً يبدو أن هناك بعض الصعوبة، بسبب اللجوء للحل العددي للمعادلة. ولكن باعتبار أن مبدأ تصميم الإسطرلاب يقوم على فكرة المحاكاة في المستوي، فجميع المنحنيات المرسومة على وجه الإسطرلاب تمثل مسقطاً للمدارات في الفراغ على المستوي. هذه المنحنيات تمكننا من إيجاد حل للمعادلة السابقة بأسلوب ميكانيكي. وبالنسبة لموقع محدد للراصد فإن قيمة a ثابتة، وبالتالي يمكن إعداد حلول مسبقة للمعادلة، تعطي العلاقة بين الزمن والارتفاع h. هذه الحلول تمثلت بمجموعة منحنيات على ظهر الإسطرلاب (الشكل 8) تعطي اتجاه القبلة في عدة مواقع جغرافية مفروضة. ولكن هذه المنحنيات رسمت كم ذكرنا باستخدام الحل الميكانيكي بالإسطرلاب نفسه، أي يمكن القول أن الإسطرلاب يصمم نفسه.

 

 

 

 

 

 

 

 

 

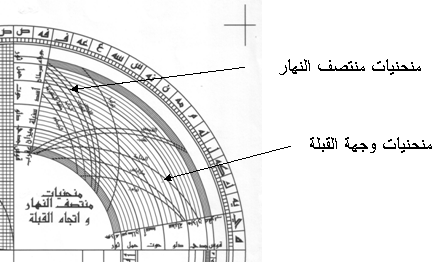
الشكل 8

 

في الواقع إن هذه المنحنيات غير دقيقة تماماً، بسبب الفرق بين منحني القبلة الحقيقي (منحني معقد) الذي يجب أن يكون مرسوماً على ظهر الإسطرلاب وما هو موجود فعلاً (منحني دائري) (الشكل 9)، ويقول كينغ[1] إن هذا الفرق يمكن أن يصل بقيمته المطلقة إلى /1°/.

بالإضافة لذلك نذكر أيضاً أن هذه الطريقة لا تصلح لكل الأماكن، بل يشترط في المكان أن تدل الشمس فيه على اتجاه القبلة وهي فوق الأفق، وهذا بدوره يتعلق بالوضع الجغرافي النسبي بين المكان ومكة المكرمة.

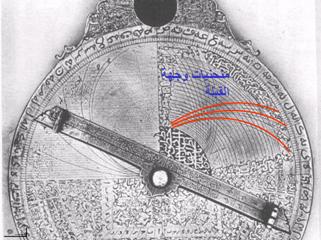
(الشكل 9)

 

تطبيق

ليكن المطلوب تحديد اتجاه القبلة باستخدام الإسطرلاب نهاراً في مدينة القدس ذات الإحداثيات: j = 31° 47'     ,      l = 35° 14' ، وذلك بتاريخ 18/8 ميلادي.

إن حل هذه المسالة رياضياً يتطلب:

1.    حساب a من العلاقة (3) بناءً على إحداثيات كل من القدس ومكة المكرمة.

2.    تحديد قيمة الانحراف d بالحساب أو من الجداول الفلكية بناءً على التاريخ.

3.    حل المعادلة (4) لتحديد h وهو ارتفاع الشمس عندما تكون باتجاه القبلة.

أما بالإسطرلاب فإن المراحل السابقة تحل كلها ميكانيكياً بسرعة وسهولة دون أي حساب كما يلي:

1.    على ظهر الإسطرلاب ومقابل التاريخ الميلادي نقرأ مباشرة موقع الشمس في بروجها. (25 السرطان)

2.    بدلالة الأخير وباستخدام منحني القبلة الخاص بالقدس نقرأ قيمة h المطلوبة. (h = 70°)

3.  نضع رأس (مري) العضادة على قيمة الارتفاع الناتجة (70°)، ونعلق الإسطرلاب شاقولياً، وننتظر إلى أن يمر ضوء الشمس من ثقبتي العضادة، مما يدل على بلوغ الشمس ذلك الارتفاع وعندها تكون باتجاه القبلة.

إن الخطوات المنفذة بالإسطرلاب والبديلة عن الحلول الرياضية لا تستغرق أكثر من ثلاث دقائق، وهذا أسرع من استخدام الطرق الرياضية والأجهزة المساحية الحديثة، ولكن طبعاً بدقة أقل، وتبقى في حدود المقبول. 

الخاتمة

بالرغم من وجود الإسطرلاب في المتاحف، إلا أنه لم يفقد أهميته العلمية، ويمكن اعتبار الإسطرلاب آلة جامعة، ويمكن استخدامها في حل العديد من المسائل الفلكية والرياضية والمساحية المعاصرة في حدود معينة للدقة. وفي هذه الورقة تم التركيز على مسألة واحدة فقط من المسائل التي تحل بالإسطرلاب وهي اتجاه القبلة. ولا يزال بالإمكان تناول هذه الآلة بالكثير من البحث.

 المراجع

باللغة العربية

1        المراكشي الحسن ابن علي ابن عمر، جامع المبادئ والغايات في علم الميقات (نسخة مصورة)، 1984، معهد تاريخ العلوم العربية والإسلامية، فرانكفورت، جزءان.

2                      بيلاني حسن، 1996 ، الجيوديزيا (الارتسامات). منشورات جامعة حلب، حلب، 259 ص.

3                      لورتش ريتشارد، رسالة نصر بن عبد الله في استخراج سمت القبلة، مجلة تاريخ العلوم، العدد

4        البيروني محمد بن أحمد – استيعاب الوجوه الممكنة في صنعة الإسطرلاب. مجلس شورى إيران، معهد التراث العلمي العربي، ميكروفيلم رقم 711 ، 125 ورقة.

5        الصوفي عبد الرحمن بن عمر بن محمد – كتاب العمل بالإسطرلاب. مخطوطة مكتبة طوب قابو سراي/أحمد الثالث، 3509، 519 ص.

6        الصوفي عبد الرحمن بن عمر بن محمد – رسالة في العمل بالإسطرلاب. مخطوطة مكتبة السليمانية/أيا صوفيا، 2642، 129ص.

 

باللغة الأجنبية

7.  King David A, WORLD-MAPS FOR FINDING THE DIRECTION AND DISTANCE TO MECCA, NETHERLAND, 1999.

8.  JOHN P . SNYDER , 1989 - An album of map projections. U. S . Geological survey, Denver , 240.

9.   PHILIP G . , 1973 - Coordinate system and map projections . London , 255 .

10.  Meeus Jean. 1991 - Astronomical Algorithms. Willmann-Bell, 

    Richmond, Virginia, 429 p.